Когда я был студентом, мне часто приходилось слышать споры о том, что тот или иной предмет - пустая трата времени, и в жизни никогда не пригодится. Чаще всего споры шли между студентами и преподавателями, причем студентами, как правило, не познавшими науку. А центром обсуждения мог стать любой предмет: как линейная алгебра или дискретная математика, так основы макроэкономики или же инженерная графика. Причем на долю последней доставалось очень много. Сейчас, по прошествии полутора десятков лет, мне иногда приходится отвечать на вопрос: "тебе пригодилась инженерная графика?" Мой ответ - да. Он обусловлен тем, что я точно понимаю, что не имея этой основы, мне бы не дались такие серьезные предметы, как детали машин или теория механизмов и машин. И дело не в умении чертить, дело в развитии трехмерного мышления, чему инженерная графика способствует очень сильно.
Чем инженерная графика может помочь на практике
Но я буду немного лукавить, если не скажу, что в основном, нападки на инженерку были связаны в большей степени с начертательной геометрией. А поскольку инжграф является прочным сплавом из черчения и начертательной геометрии, то защищая инженерную графику, мне придется защищать именно начертательную геометрию, т.к. полезность черчения из года в год ставится под сомнение разве что студентами с факультетов маркетинга или экономики.
Этим летом ко мне обратились сразу два человека с просьбами помочь на практике решить их задачи. И это при том, что я нигде на сайте не позиционирую свои знания как путь к решению реальных проблем. Однако эти мужики понимали, что именно знания в начерталке (пусть и на аутсорсинге) дадут им ответы на их вопросы.
Задача первая.
Крыша едет, инженерная графика рулит.
Была построена банька. И это хорошо. Но для завершения строительных работ необходимо вывести через крышу трубу. А крыша имеет уклон, угол которого известен. Вопрос заданный мне звучал так: "как мне на крыше разметить отверстие для трубы?".
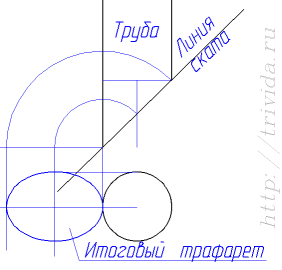
Задача является классическим элементом инженерной графики. Сводится она к поиску натурального вида линии пересечения цилиндра с наклонной плоскостью. Т.е. в моем случае это было бы так: 5 минут на то чтоб начертить на компьютере сечение, еще пять минут - на распечатывание и склеивание (не у каждого есть возможность печати на форматах А3 и больше). После чего остается только вырезать и наложить полученный шаблон в нужное место крыши, после чего обвести. Итого - 10 мин, а на выходе - идеально размеченное выходное отверстие в крыше, что значительно облегчит последующее заделывание щелей.
Задача вторая.
Инженерная графика: знания на бочку!
Обратившийся человек занимается время от времени сваркой конструкций из труб. При сваривании труб под нестандартными углами ему требуется на двух концах свариваемых труб выполнить срез под нужным углом, да так, чтоб при прикладывании двух срезов друг к другу получались как можно меньшие зазоры. Диаметр же труб не предполагает обычного распиливания ножовкой под заданным углом. В описываемом случае он варил конструкцию из бочек диаметром 600 мм и вопрос заключался в том, как нанести на бочку линию среза ее плоскостью под заданным углом. Потратив время на поиски простого решения он написал мне. Я сам удивился, когда инженерная графика позволила элегантно решить и эту задачу. Суть способа сводилась к построению развертки цилиндра, с нанесенной на него линией пересечения цилиндра и плоскости.
Опять же, опишу свои действия, будь это моя задача.
1. Подготовить лист для чертежа развертки. Подойдет остаток старых обоев или лист рубероида, если в избытке, упаковочная бумага или еще что-либо, не сильно тянущееся. Обмотать им трубу, для определения точной длины внешней окружности и определения границ развертки цилиндра.
2. Построить на компьютере математически точный чертеж пересечения цилиндра с наклонной плоскостью.
3. Построить математически точный чертеж развертки цилиндра с нанесенной на него линией пересечения с плоскостью.
4. Полученный на ПК чертеж развертки аккуратно перенести с масштабированием на приготовленный лист. Срезать верхнюю часть.
5. Приложить к бочке получившуюся развертку, обвести по верхнему краю.
В итоге должна получиться линия на бочке или трубе, идеально лежащая в плоскости под заданным углом.
Надеюсь, эти два примера помогут вам поверить в то, что инженерная графика и начертательная геометрия имеют вполне себе практическое применение. А помножив это на влияние начерталки на развитие способностей к представлению в уме трехмерных моделей - тут уже у вас не должно оставаться сомнений в необходимости серьезного отношения к предмету. Желаю вам удачи в учебе, а также интересного применения на практике полученных знаний!




