|
Разделы Уроки по теме Рекомендуем |
 Построение линии пересечения конуса и плоскости Автор: Moroz Дата: 2012-07-27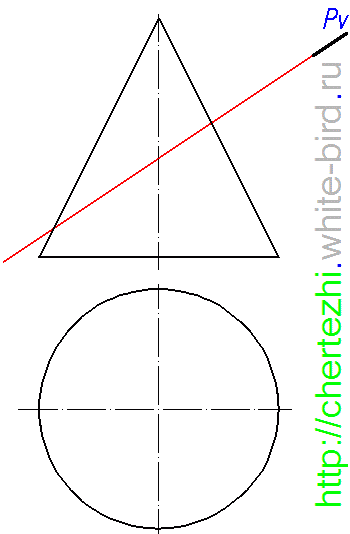 
Вслед за уроком, в котором я рассказывал вам, как построить линию пересечения цилиндра с наклонной плоскостью, пришло время опубликовать статью о построении линии пересечения конуса и наклонной плоскости. Умение построить линию пересечения конуса с плоскостью может пригодится вам при построении натурального вида фигуры сечения или же просто, при решении простой задачи о сечении конуса. В любом случае, в курсе инженерной графики вы как минимум раз с этим столкнетесь. Так пусть же это столкновение пройдет для вас менее болезненно. В противном случае, пишите, звоните, будем договариваться :) Итак, приступим. На рисунке ниже вы видите среднестатистический чертеж в том виде, в котором вы получаете задание на сечение конуса плоскостью. С той лишь поправкой, что обычно на нем не изображен третий вид. Его я начертил заранее, подготовив для будущих построений. 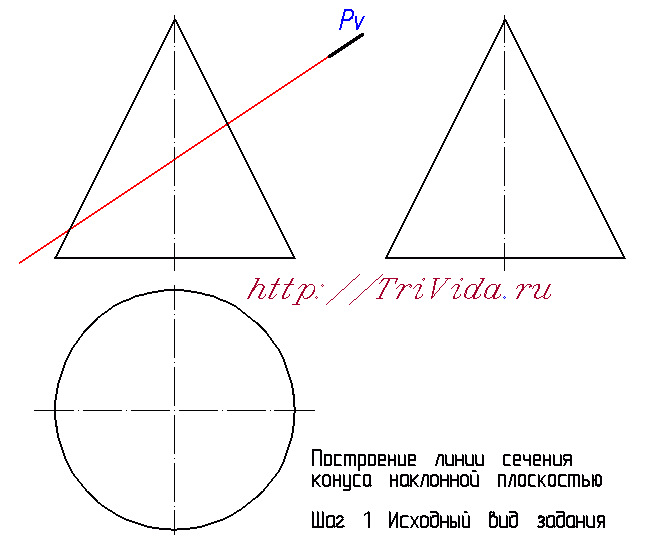 Первым делом обозначим точки, в которых плоскость пересекает образующие конуса на фронтальной проекции. Снесем их на горизонтальную проекцию до пересечения с осью, а так же на профильную проекцию - так же до пересечения с осью. Отмечу, что точка 2'' будет невидимой (на рисунке это явно не указано). 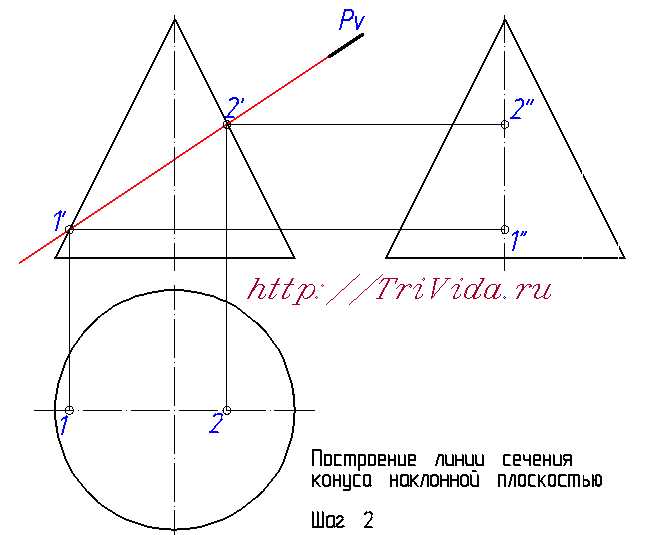 Пришло время сказать кое-какие важные вещи, касаемые того, какие бывают типы сечений конуса. Их четыре:
Но если про элипс в сечении вы скорее всего знали, или догадывались, то вот насчет его центра очень многие ошибаются. Хотя казалось бы, поиск центра элипса в нашем случае не должен доставлять хлопот. Внимательно читаем и запоминаем: центр элипса в данном случае находится ровно посередине между точками 1 и 2. Поскольку 1-2 является одной из осей элипса. Большой или малой - зависит от наклона секущей плоскости и практического значения для нас сейчас не имеет. 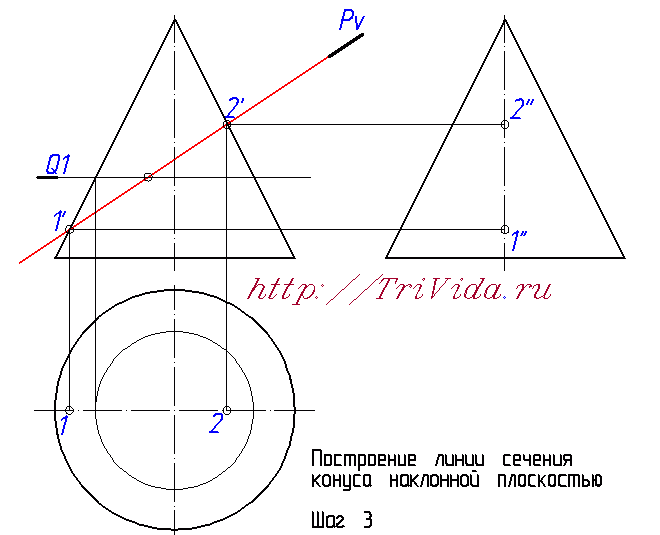 Обозначим точки пересечения этой вспомогательной плоскости Q1 с проекцией наклонной плоскости Pv на фронтальной проекци, получим точки 3' и 4'. Из них опускаем линию связи вниз, до пересечения с окружностью, получаем точки 3 и 4. Отрезок 3-4 является второй осью элипса. 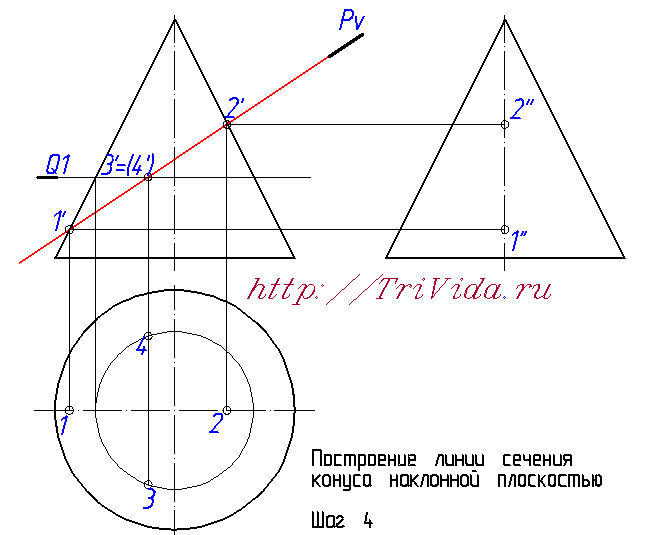 Чтобы построить профильные проекции этих точек, проводим из проекции точек 3' и 4' линию связи вправо, на профильную проекцию. И затем, на ней откладываем от оси конуса отрезки, обозначенные синим и зеленым цветом. Такой же длины, как синий и зеленые отрезки обозначенные на виде сверху (на горизонтальной проекции). Получаем точки 3" и 4". 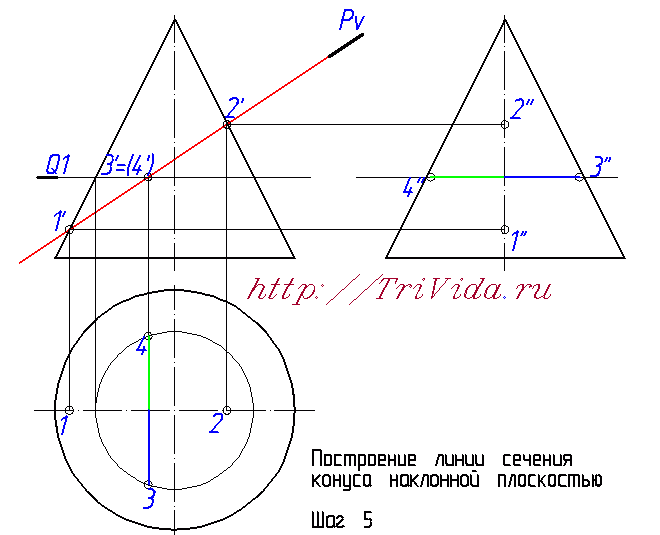 Математически на основе знаний о двух осях мы могли бы построить элипсы на горизонтальной и профильной проекциях. Но поскольку нам не удастся убедить преподавателя, что мы роботы, способные построить элипс опираясь только на 4 точки, мы вынуждены построить несколько дополнительных точек. На рисунке, изображающем 6-й шаг построения мы провели вспомогательную секущую плоскость Q2, в произвольном месте, где-то посередине между центром элипса и точкой 2'. C ее помощью (ориентируясь на алгоритм описанный при построении точек 3 и 4) определили все проекции точек 5 и 6. 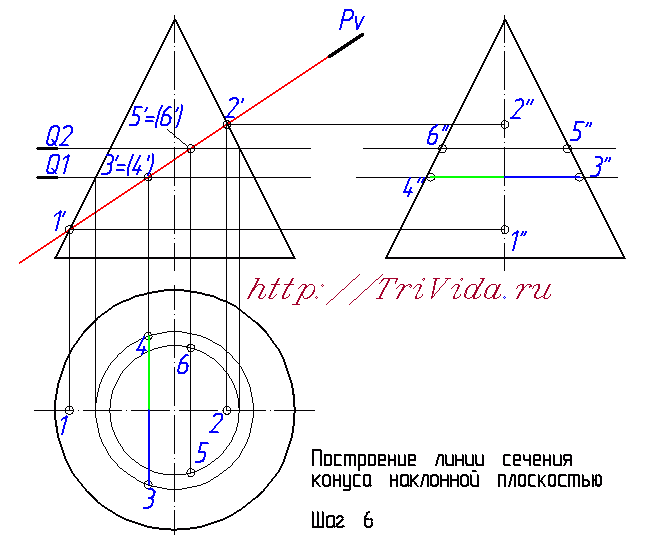 Точно так же проводим вспомогательную плоскость Q3 ниже точки 3' и выше точки 1' и с ее помощью находим все проекции точек 7 и 8. Теперь у нас уже есть 8 точек, чего вполне достаточно для более-менее точного построения от руки элипса не очень больших размеров. Если же у вас конус большой, то возможно вам имеет смысл провести еще некоторое количество вспомогательных секущих плоскостей и построить дополнительные точки. 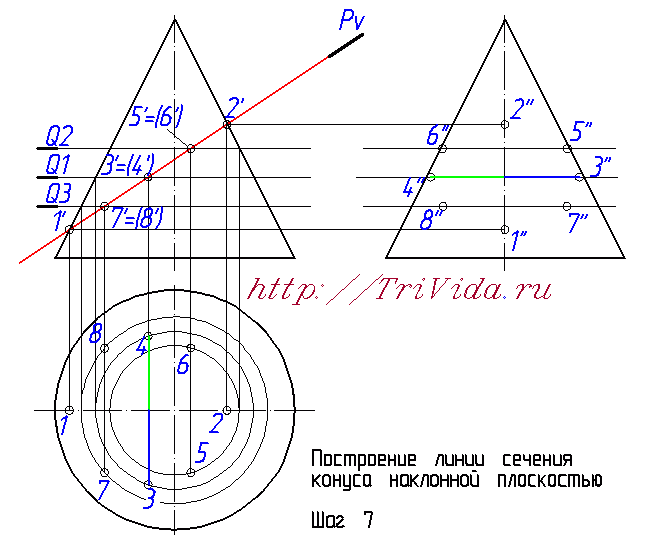 Остался еще один важный момент - определение точек границ видимости элипса на третьем виде. Для этого надо провести из точки пересечения плоскости Pv с осью элипса линию связи направо, на профильную проекцию. В местах, где эта диния пересекается с образующими конуса как раз и будут искомые точки. На чертеже я их никак не обозвал, вы же можете дать им имена 9" и 10". Та часть элипса, что будет за ними, будет находиться за конусом и соответственно будет невидидима. 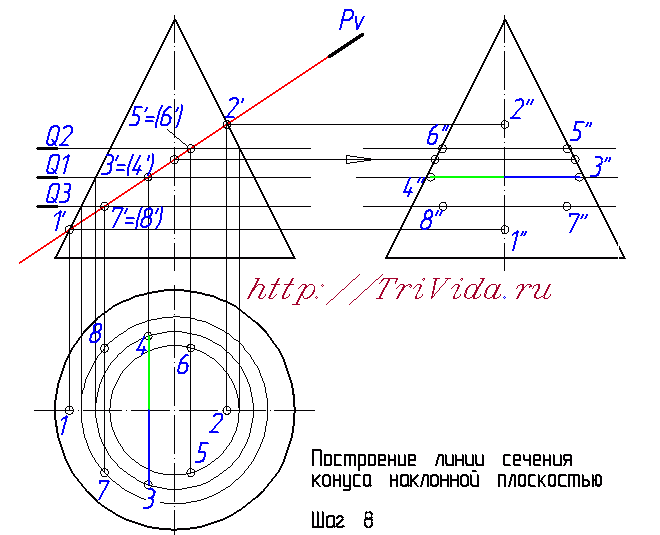 Проведем элипсы через полученные точки на горизонтальной и профильных проекциях: 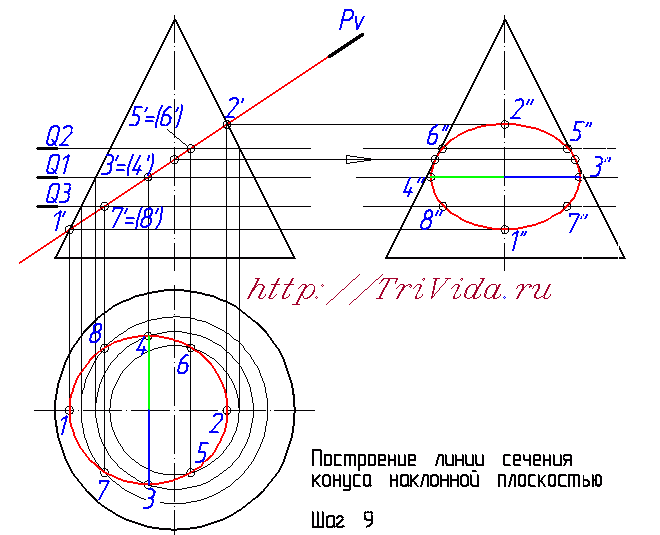 Последним этапом, завершающим построение линии пеерсечения Конуса с наклонной плоскостью, будет обозначение видимости элипса на профильной проекции: 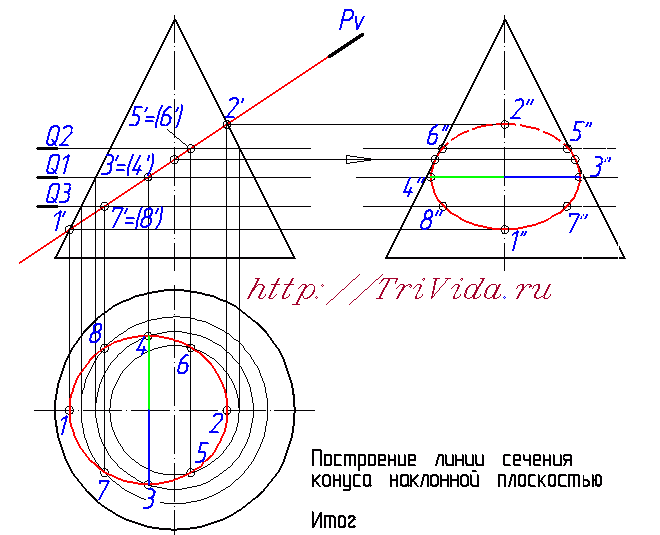 На этом месте я объявляю перерыв, и мне лишь остается выразить надежду, что этот урок принес вам реальную пользу при решении своих домашних заданий. Лишь бы было у вас время прочесть весь этот материал и внимательно рассмотреть сопровождающие его рисунки. В блишайшем уроке я планирую рассмотреть выполнение задания по нахождению натуральной величины сечения, так что велкам снова :) Просмотров: 186580 Вы можете сказать "спасибо!" автору статьи: пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект "White Bird. Чертежи Студентам" или или запишите наш телефон и расскажите о нас своим друзьям - кто-то наверняка ищет способ выполнить чертежи или создайте у себя на страничке или в блоге заметку про наши уроки - и кто-то еще сможет освоить черчение. А вот это - не реклама. Это напоминание, что каждый из нас может сделать. Если хотите - это просьба. Мы действительно им нужны:  Комментарии: Автор комментария: Ольга Большое спасибо за подробный пример, но было бы лучше, если бы разобрали сложный пример. Автор комментария: Василий Огромнейшее спасибо за изложенный пример. Мне это очень помогло. Автор комментария: Михаил Отличный пример!
Сэкономил массу времени:)
Автор комментария: Анастасия Как провести элипсы через полученные точки? ( шаг 9) Автор комментария: Валентина Огромное спасибо!!!Давно закончила институт, а тут пришлось повспоминать начерталку, чтобы помочь внуку. Все получилось. Еще раз большое спасибо! Автор комментария: Александр Что делать если плоскость не частного, а общего положения, да еще и задана треугольником?
Автор комментария: Наталья Спасибо огромное за данный урок! Мне это очень помогло! По крайней мере свою задачу я кое-как, но все же решила! :) Спасибо еще раз!
Автор комментария: артем Вот бы нам так на парах объясняли было бы в разы интереснее Спасибо, Артем! Уверен, что каждый человек способен рассказывать и понятно, и интересно. Если он влюблен в свое дело. Автор комментария: Евгений Присоединяюсь ко всем благодарностям, конечно же, но..)) хотел бы спросить. Для варианта, когда секущая плоскость параллельна одной из образующих, как построить сечение без профильной проекции? Ранее строил такой рисунок без нее, вдобавок смотрю решение этого же рисунка без присутствия профильной проекции (даже стертых следов от карандаша не наблюдаю) %) Если конкретнее, то как на горизонтальной проекции сечения найти расстояние от горизонтальной оси до точек на линии связи, проведенной с фронтальной проекции? Собственно, вот этот начерченный рисунок (если не затруднит, объясните, пожалуйста, для варианта с секущей плоскостью "сигма 2". Автор комментария: Евгений Забыл про рисунок. Вот он http://dfiles.ru/files/e83yaz9ys Но, как обычно, после написания сообщения, понял, что необходимо пользоваться радиусами, отмеренными от оси до образующей конуса в месте пересечения вспомогательной плоскости)) но сообщения могут пригодится для таких нерасторопных как я)) Да, это известный способ находить правильное решение по ходу формулирования вопроса :) На всякий случай для всех напишу: В разобранном мной в статье примере третий вид представлен только для полноты картины, поскольку часто просят решить в трех проекциях. Но если третья проекция не нужна - мы ее просто не чертим, работаем только с главным видом и видом сверху. Автор комментария: Ольга спасибо огромное Автор комментария: Willy Скажите,пожалуйста,сколько радиусы внутренних кругов? Радиусы внутренних кругов получаются путем переноса по линии связи точек пересечения на фронтальной проекции вспомогательных горизонтальных плоскостей с образующей конуса. Линия связи проводится до линии оси окружности, являющейся горизонтальной проекцией основания конуса. Автор комментария: доня огромнейшее спасибо за полезные уроки, что бы я без вас делала Автор комментария: Татьяна Большое спасибо за разъяснения. Вы очень помогли. Автор комментария: Юлия Действительно большое подспорье для студентов! Ведь не всегда есть возможность достать книги по начертательной геометрии и черчению. Большое, даже сказала бы огромное СПАСИБО!!!! :-) Юлия, даже боюсь предположить, что бы было, если бы у меня была возможность по-человечески расписать оставшиеся нераскрытыми темы :) Вам спасибо - вы читаете и цените. Автор комментария: Алексей Спасибо огромное! Чертить не умею, все чертеж что были необходимы в процессе учебы заказывал... на экзамен дали чертить такое вот задание, и если б не Ваш наглядный и понятно изложенный пример был бы карачун мне! Огромное спасибо, все сделалось очень даже просто :) Скажите ведь, интересный случай! Алексей, вы молодец.С опозданием - но самостоятельно, с использованием, так сказать, литературы! Если бы все вернуть назад - глядишь - и остальные задания осилили бы :) Автор комментария: ирина а если секущая плоскость введена на виде сверху? Ирина, спасибо за интересный вопрос. Если плоскость введена на виде сверху, то вы делаете те же действия, но наоборот: сначала проводите концентрические окружности - как бы следы от вспомогательных секущих плоскостей, потом из точки пересечения этих окружностей с осью конуса, параллельной оси ох, проводите линии связи наверх, до пересечения с образующей конуса. Из полученной точки проводите горизонтальную секущую плоскость. Вернувшись в вид сверху ищете точки пересечения вашей окружности с линией, задающей сечение. Из нее проводите наверх линию связи, до пересечения с полученной секущей плоскостью. Это уже будет точка принадлежащая линии пересечения. Самое интересное: как найти самую ближнюю к оси конуса, самую высокую точу сечения. Для этого нужно провести на виде сверху перпендикуляр к секущей плоскости. Через полученную точку провести касательную окружность. Это будет самая маленькая из вспомогательных окружностей, обозначающих вспомогательные секущие плоскости. Выполнив с ней все действия, описанные в этом комментарии вы получите на виде сверху самую высокую точку вашей гиперболы. Автор комментария: Вероника Огромное Вам спасибо! Для заочной формы обучения такой материал - отличное подспорье. И здорово, что рассмотрены три проекции, тк в моем задании требуется построить фронтальную, горизонтальную, профильную проекции + натуральную величину сечения. Автор комментария: Алла Спасибо огромное за ваше время и такой доступный материал, столько всего перелопатила, а результата ноль. Я очень рада , что попала на ваш сайт , теперь ваша страничка у меня в избранном, прям как палочка-выручалочка. Кстати после завтра экзамен, задание схожее только с разными вырезами. Я думаю начерчу без проблем. Еще раз СПАСИБО!!! Автор комментария: Михаил Благодарен! Успехов Вам! Автор комментария: ЭРКЕБУЛАН как найти точку е" Автор комментария: Мария Спасибо!!! Выручили и доступно объяснили! Автор комментария: Дмитрий Спасибо, ваш урок очень помог! У меня линия сечения конуса изображена снизу, в итоге гипербола. Теперь вот надо найти натуральную величину сечения, не знаю алгоритма, с чего начинать. Дмитрий, спасибо за отзыв! К сожалению, у меня пока нет статьи, как построить натуральный вид сечения конуса. Наиболее близкий материал вы можете найти в этом уроке Автор комментария: Дмитрий Скажите пожалуйста, чему равен радиус окружности,на которой лежат точки 3 и 4 Вспомогательная секущая плоскость Q проводится на произвольной высоте. Линия связи опускается вниз из точки пересечения Q с образующей конуса. С помощью этой линии связи мы и определяем радиус по которому вспомогательная плоскость пересекает конус. Автор комментария: Никита Здравствуйте, не могли бы вы пояснить, как делать сечение наклонной четырехгранной пирамиды при условии, что секущая плоскость дана на виде сверху? Автор комментария: Андрей Спасибо большое , очень помогло Автор комментария: Ленар Спасибо огромное за данный урок! Автор комментария: Виктория Материал очень помог, спасибо! Но как решить подобную задачу, если в сечении должен быть не эллипс, а дуга эллипса? (больше половины) Виктория, присылайте картинку на почту или в группу в Вконтакте, посмотрим вместе. Автор комментария: Кирилл А как же случай с наклонным конусом? Автор комментария: Женя А как найти уравнение елипса, образованного сечением плоскости в точке, удалённой на l от вершины, под углом альфа, зная высоту конуса и его радиус? Автор комментария: Женя А как строить гиперболу? Гипербола ведь получается не только, когда секущая строго паралельна оси конуса - но и в промежутке, когда секеущая находится между положением паралельно оси конуса, и положением, когда секущая касается образующей конуса. Добавьте свой комментарий: |
Последние уроки Как построить диметрию детали? Построение наклонного сечения, заданного на виде слева Определение линии пересечения двух плоскостей. Метод вспомогательных секущих плоскостей. Наша почта: zakaz@trivida.ru Наша страница в ВК:  Случайный комментарий Кирилл: Антон, приветствую! Нам с вами поставили "5-" )) Спасибо вам ещё раз. Кирилл, пятерочка - это замечательно! Не зря мы ворошили вашу начертательную геометрию, не зря! Тут, как говорится, главное не перестараться и не сделать на 6 :) |
При публикации статей с сайта активная ссылка на оригинал обязательна.