|
Разделы Уроки по теме Рекомендуем |
 Точка пересечения прямой и плоскости Автор: Moroz Дата: 2010-09-30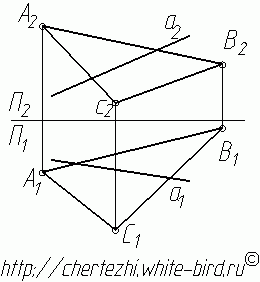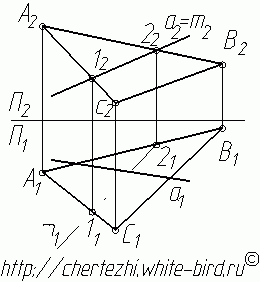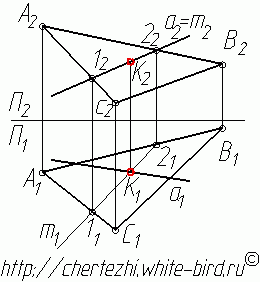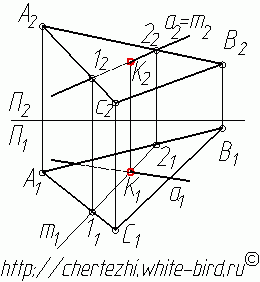 
Рассмотрим пошаговую инструкцию построения точки пересечения прямой общего положения с плоскостью общего положения.Отметим, что построение точки пересечения прямой и плоскости - это одна из основ решения задач по предмету начертательная геометрия, не освоив которую дальнейшее понимание предмета будет достаточно трудным. Порядок построения точки пересечения прямой и плоскости
1. Заключим прямую а во вспомогательную фронтально-проецирующую плоскость (плоскость перпендикулярную фронтальной плоскости проекции). На фронтальной проекции она сольется с прямой а. Очевидно, что линия m пересечения этой плоскости с плоскостью треугольника АВС на фронтальной проекции так же будет сливаться с прямой а (а=m). Обратите внимание, что мы начали поиск точки пересечения прямой с плоскостью с того, что заключили прямую а во вспомогательную фронтально-проецирующую плоскость. Точно таким же образом можно было заключить прямую а в горизонтально-проецирующую плоскость, и тогда бы построения начались как бы "снизу вверх", но смысл остался бы точно таким же, как и конечное решение - точка пересечения прямой с плоскостью.
Внимание! Для этой темы есть видеоурок. Просмотров: 247580 Вы можете сказать "спасибо!" автору статьи: пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект "White Bird. Чертежи Студентам" или или запишите наш телефон и расскажите о нас своим друзьям - кто-то наверняка ищет способ выполнить чертежи или создайте у себя на страничке или в блоге заметку про наши уроки - и кто-то еще сможет освоить черчение. А вот это - не реклама. Это напоминание, что каждый из нас может сделать. Если хотите - это просьба. Мы действительно им нужны:  Комментарии: Автор комментария: Дмитрий Очень легко и понятно вы описали как найти точку пересечения прямой и плоскости, мегареспект! Автор комментария: Алексндр Да, теперь осилил Автор комментария: Студент Сделайте нормальные чертежи!!! Без анимации пошаговые. Автор комментария: Михаил А вот нечего торопиться. Надо покушать как следует, сесть и всмотреться в гифку. Тогда и познаешь дзен. :) Не торопиться, быть сытым и выспавшимся - да, это отличное подспорье. Спасибо за то, что указали на столь важные моменты. Да прибудет с вами сила, Михаил! Автор комментария: Настя Помогите пожалуста!!!!!!у меня плоскость перпендикулярна фронтальной плоскости проекции и задана следами, а прямая горизонтальна горизонтальной плоскости проекций Автор комментария: Евгений Это простооо кул,все понятно,мегареспект вам!! Автор комментария: Георгий 4. Соединим горизонтальные проекции точек 1 и 2 - получим горизонтальную проекцию прямой m (которая является точкой пересечения вспомогательной плоскости с плоскостью треугольника АВС... Тут надо исправить: прямая не может являться точкой. Также отсутствует закрывающая скобка. Автор комментария: Дмитрий Я всё равно ничего не понял. Хоть на первый взгляд это более толковое объяснение решения, чем пишут в книгах - там ваще мрак. Автор комментария: Лиля Высший класс! Ключевое предложение для понимания сути: "Заключим прямую а во вспомогательную фронтально-проецирующую плоскость ..." Эмм... Это сарказм? :) Если да, то в свое оправдание могу сказать лишь то, что терминология должна быть вам в некоторой мере знакома. С меня лишь графический порядок решения. Но с другой стороны давать его в абсолютном отрыве от теории тоже нехорошо. Указанная в вашем комментарии фраза пригодится вам на экзамене, или как минимум на защите данной работы. Но для графического решения прямо сейчас она не так важна. Просто выполняйте по шагам. Автор комментария: Лия Спасибо!!! Автор комментария: Василий Спасибо огромное.Всё доходчиво и ясно! Автор комментария: Олег Как быть если прямая на П2 перпендикулярна Ох, а на П1 в точку проэцируется? Автор комментария: Умед Здравствуйте Добавьте свой комментарий: |
Последние уроки Как построить диметрию детали? Построение наклонного сечения, заданного на виде слева Определение линии пересечения двух плоскостей. Метод вспомогательных секущих плоскостей. Наша почта: zakaz@trivida.ru Наша страница в ВК:  Случайный комментарий Сергей: Всем, кто будет в будущем решать, звонить сюда, или кому-то еще - однозначно говорю - сюда. Есть с чем сравнить. В прошлом году заказывал начертательную геометрию в другом месте - устал звонить чтоб отдали чертежи и методичку. Здесь же - отдали готовые чертежи день в день как изначально договорились. Чертежи чистые и препод даже не придрался, хотя меня и предупредили, что могут попросить что-то немного подправить. Еще раз спасибо, очень выручили. Сергей, благодарю вас, что нашли время отписаться. Кстати о времени - нелегко было сделать ваши пять листов за один день. Старайтесь впредь так не затягивать! Обращайтесь, если еще будет нужно, хотя черчение у вас уже закончилось.. |
При публикации статей с сайта активная ссылка на оригинал обязательна.